以下の本を読んでガウス過程回帰について勉強したので、実際にpythonで実装してみました。

ガウス過程と機械学習 (機械学習プロフェッショナルシリーズ)
圧倒的に柔軟なベイズ的回帰モデルであるガウス過程の日本初の入門書。基礎の線形回帰から始め、ガウス過程の原理をゼロからていねいに解説。教師なし学習、実応用など最近の話題まで紹介した。さあ、はじめよう!
1変数
sklearnでいうところの、RBFカーネル+Whiteカーネル(観測ノイズ)をkernelクラスとして記述しています。
sklearnのカーネルリスト
- sklearn.gaussian_process.kernels.CompoundKernel
- sklearn.gaussian_process.kernels.ConstantKernel
- sklearn.gaussian_process.kernels.DotProduct
- sklearn.gaussian_process.kernels.Exponentiation
- sklearn.gaussian_process.kernels.ExpSineSquared
- sklearn.gaussian_process.kernels.Hyperparameter
- sklearn.gaussian_process.kernels.Kernel
- sklearn.gaussian_process.kernels.Matern
- sklearn.gaussian_process.kernels.PairwiseKernel
- sklearn.gaussian_process.kernels.Product
- sklearn.gaussian_process.kernels.RationalQuadratic
- sklearn.gaussian_process.kernels.RBF
- sklearn.gaussian_process.kernels.Sum
- sklearn.gaussian_process.kernels.WhiteKernel
全コード
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
class kernel:
def __init__(self, s1=1.0, s2=1.0, s3=0.1):
self.s1, self.s2, self.s3 = s1,s2,s3
def rbf_white(self,x, x_p,i=1):
"""カーネル計算"""
# cdist:n-ベクトル間のユークリッド距離
if i ==1:
k = self.s1 * np.exp(-1.0 * cdist(x, x_p, 'sqeuclidean')/self.s2) + (self.s3 * np.eye(x.shape[0]))
else:
k = self.s1 * np.exp(-1.0 * cdist(x, x_p, 'sqeuclidean')/self.s2)
return k
# サンプルデータの作成
x_train = np.expand_dims(np.random.uniform(-10,10,20), 1) # 学習データ
x_test = np.linspace(-10,10,100).reshape(-1,1) # テストデータ
y_train = np.sin(x_train)
# 計算準備
kernel = kernel()
k11 = kernel.rbf_white(x_train,x_train)
k12 = kernel.rbf_white(x_train,x_test,0)
k22 = kernel.rbf_white(x_test,x_test)
k11_inv = np.linalg.inv(k11)
# 期待値
y_test = np.dot(k12.T, np.dot(k11_inv, y_train))
# 分散
vars = k22 - np.dot(k12.T, np.dot(k11_inv, k12))
# 標準偏差
y_test_std = np.sqrt(np.diag(vars)).reshape(-1,1)
# 結果の作図
fig,ax = plt.subplots(figsize=(8,6))
ax.scatter(x_train,y_train,label="train")
ax.plot(x_test, y_test, label="test")
ax.plot(x_test, np.sin(x_test),label="true")
plt.fill_between(x_test.flatten(), (y_test + y_test_std).flatten(), (y_test - y_test_std).flatten(), alpha=0.3)
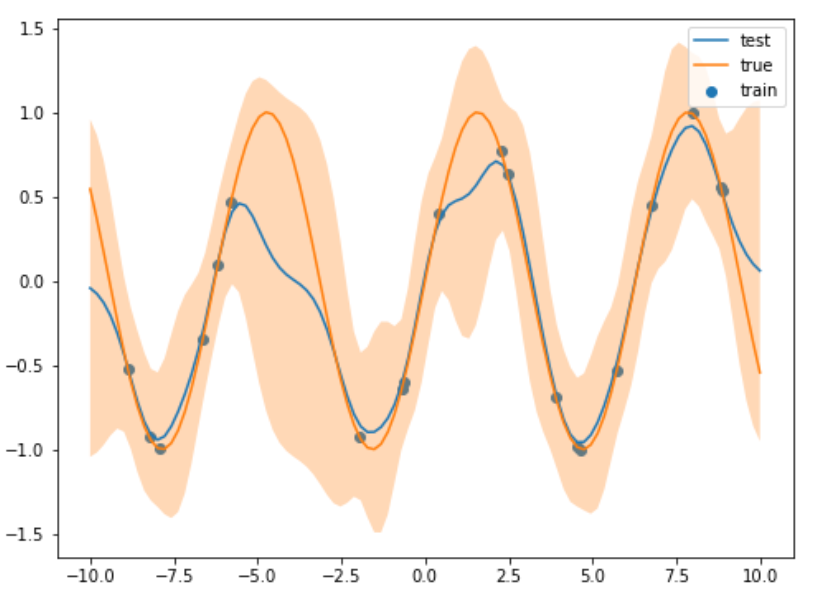
ax.legend()割といい感じにできているように見えます。
2変数
2変数の場合でもコードは同じです。
標準偏差は可視化できていませんが、おおむね回帰できているように見えます。
# サンプルデータの作成
x1_train = np.expand_dims(np.random.uniform(-10,10,100), 1)
x2_train = np.expand_dims(np.random.uniform(-10,10,100), 1)
x_train = np.append(x1_train,x2_train,axis=1)
x1_test = np.expand_dims(np.random.uniform(-10,10,50), 1)
x2_test = np.expand_dims(np.random.uniform(-10,10,50), 1)
x_test = np.append(x1_test,x2_test,axis=1)
y_train = x1_train / x2_train# 作図準備
fig = plt.figure(figsize = (8, 8))
ax = fig.add_subplot(111, projection='3d')
# 軸ラベルを設定
ax.set_xlabel("x1", size = 14, color = "r")
ax.set_ylabel("x2", size = 14, color = "r")
ax.set_zlabel("y", size = 14, color = "r")
# 描画
ax.scatter(x_train[:, 0], x_train[:, 1], y_train, s = 40, c = "blue",label="train")
ax.scatter(x_test[:, 0], x_test[:, 1], y_test, s = 40, c = "red",label="test")
plt.show()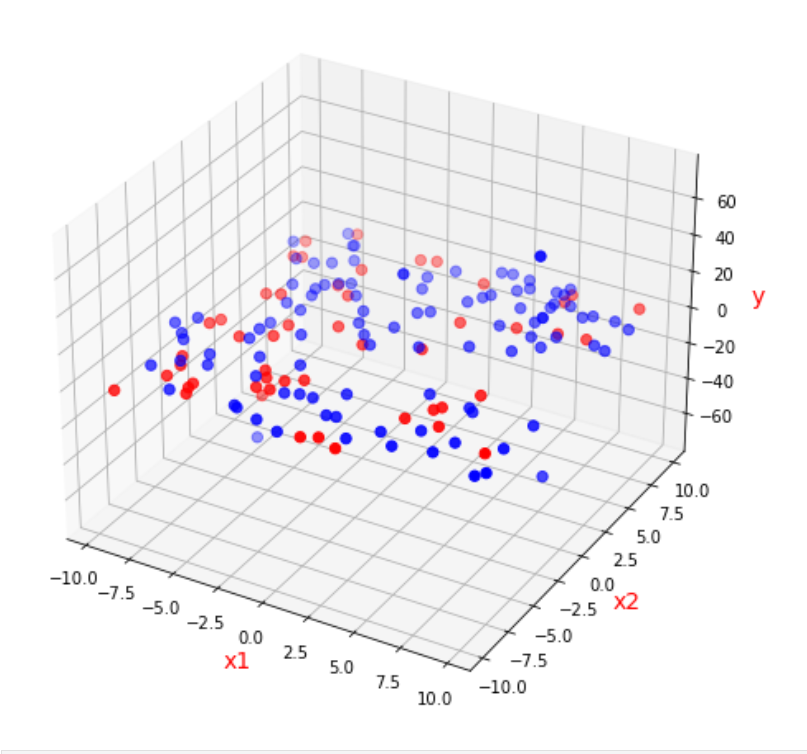


コメント