ある目的特性を得るための実験は、そのパラメータの種類の数に応じて飛躍的に探索空間が増加します。
そこで、より効率的な探索を行う手法が実験計画や品質工学といった分野で検討されてきました。
今回は、探索空間をできるだけ均一にサンプリングするラテン超方格により実験条件を設定する方法を紹介します。
今回の検討内容
パラメータA,Bについて、ラテン超方格により、一定範囲内の値でサンプリングを行います。
パッケージの準備
ラテン超方格はpyDOE2というパッケージで作成できます。
pyDOEが更新が途絶えたためか、pyDOEからフォークしたパッケージになります。
基本的な使用方法はpyDOEに準じます。
インストールはpipで可能です。
pip install pyDOE2
pyDOE2
Design of experiments for Python
pyDOE: The experimental design package for python — pyDOE 0.3.6 documentation
Design of experiments for Python
今回は、その他のパッケージとしてpandasとscikit-learnを使用します。
コード
検討したいパラメータA,Bの上下限の値を以下のように設定しました。
# 変数の上下限設定
boundary = pd.DataFrame({'paramA':[0,5],'paramB':[50,100]})boundary
pyDOE2のlhs()により、ラテン超方格が使用できます。
0から1の値が返されます。
# 2変数で10サンプルのラテン超方格の作成
# doe.lhs(パラメータ数, サンプル数, サンプリング方式, 乱数シード値)
lhs = doe.lhs(2, samples=10, criterion='center',random_state=0)変数:lhs

scikit-leranのMinMaxScalarを使用し、上記で得たlhsの値を、boundaryの上下限値に合わせます。
# 各変数の上下限に基づいてラテン超方格の値を変換
scaler = MinMaxScaler()
min_max = scaler.fit(boundary)
value = pd.DataFrame(min_max.inverse_transform(lhs), columns=boundary.columns)実行結果
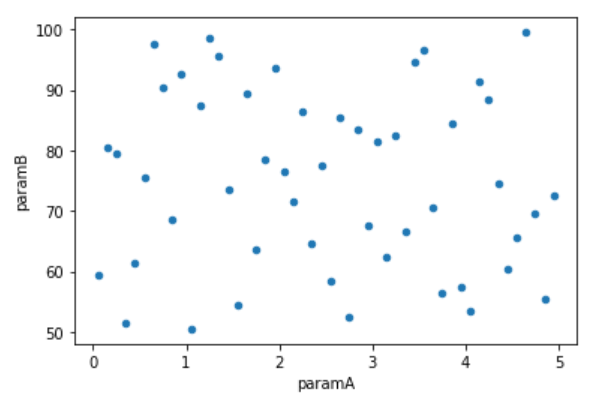
今回の実行結果では以下のようになりました。
10サンプル程度だと隙間が目立ちますが、50サンプル程度になるとある程度の全体をカバーできているように見えます。
10サンプル

50サンプル
全体コード
import pyDOE2 as doe
from sklearn.preprocessing import MinMaxScaler
import pandas as pd
# 変数の上下限設定
boundary = pd.DataFrame({'paramA':[0,5],'paramB':[50,100]})
# 2変数で10サンプルのラテン超方格の作成
lhs = doe.lhs(2, samples=10, criterion='center',random_state=0)
# 各変数の上下限に基づいてラテン超方格の値を変換
scaler = MinMaxScaler()
min_max = scaler.fit(boundary)
value = pd.DataFrame(min_max.inverse_transform(lhs), columns=boundary.columns)
# 得られた条件の可視化
value.plot.scatter(x='paramA', y='paramB')


コメント